Without an understanding of human cognitive architecture, instruction is blind.[i]
Cognitive load theory helps us to understand how people generally learn and store new information, and the types of instructional practices that best support learning. It draws on the characteristics of working memory and long-term memory and the relationship between them to explain how people learn. Cognitive load theory emerged in the late 1980s from the work of John Sweller and his colleagues. The theory is based on our knowledge of the structure and processes of the human mind, known as human cognitive architecture. Human cognitive architecture helps us understand how we learn, think, and solve problems. It is considered to be a natural information processing system that generates various procedures designed to reduce cognitive load and facilitate the acquisition of biologically secondary knowledge held in long-term memory.
The distinction between biologically primary and biologically secondary knowledge
There are two basic categories of knowledge, biologically primary and biologically secondary[ii]. Biologically primary knowledge is information humans have evolved to acquire over thousands of generations. It is acquired unconsciously without instruction because it is necessary for the survival of humans and their societies. Biologically primary knowledge includes general problem-solving and thinking skills such as learning to speak and listen in a native language at a young age, generalising, transferring, and performing simple social skills like recognising faces. Because we have evolved to acquire such information automatically, it does not need to be taught and, since we can learn biologically primary information easily, it does not impose a heavy cognitive load.
In contrast, biologically secondary knowledge relates to information that needs to be explicitly taught and not left for students to discover. It requires conscious effort, and most subjects taught in formal education belong in this category of information. Reading, writing, mathematics, history, science, and other subjects traditionally taught in schools and universities are examples of biologically secondary knowledge. Since the acquisition of biologically secondary information requires conscious effort because it does not happen easily and automatically in the same way as listening and speaking, it requires mental effort. In other words, it imposes a cognitive load.
Generic-cognitive skills and domain-specific skills
According to Sweller, most biologically primary knowledge results in generic-cognitive skills. These are basic skills that can be applied across a variety of domains. On the other hand, most of what is taught in educational institutions consists of domain-specific skills. Even though generic-cognitive skills are far more important than domain-specific skills because they contribute to an individual’s overall ability to adapt, learn and think independently, domain-specific skills are what need to be taught because they are not acquired easily and unconsciously. Biologically secondary, domain-specific skills need explicit instruction[iii] because, without it, most students will have to use a trial-and-error strategy to find the solution to a problem, and that kind of strategy imposes a heavy cognitive load.
Take as an example the specific problem-solving skills required to effectively solve the algebraic equation: 2x – 40 = 60. One way to solve this equation would be to follow two solution steps. Firstly, to add 40 to both sides of the equation to arrive at the simplified equation: 2x = 100; and secondly, to divide both sides of the simplified equation by 2 to arrive at the answer: x = 50. However, if a student attempts to solve the problem by using a trial-and-error strategy – for example, by substituting multiple values for x to eventually reach a solution – this is likely to impose a heavier burden on the working memory (or cognitive load), than if they are provided with the solution steps. This biologically secondary, domain-specific skill – in this case, the mathematical method for solving the equation – should be explicitly taught.
The relationship between working memory and long-term memory
Cognitive load theory explains the way that new knowledge is constructed in working memory, and the way that permanent knowledge is built up and held in long-term memory – it explains how we learn. Figure 1 below represents the aspects of the human memory system used to describe the separate processes associated with working memory and long-term memory.
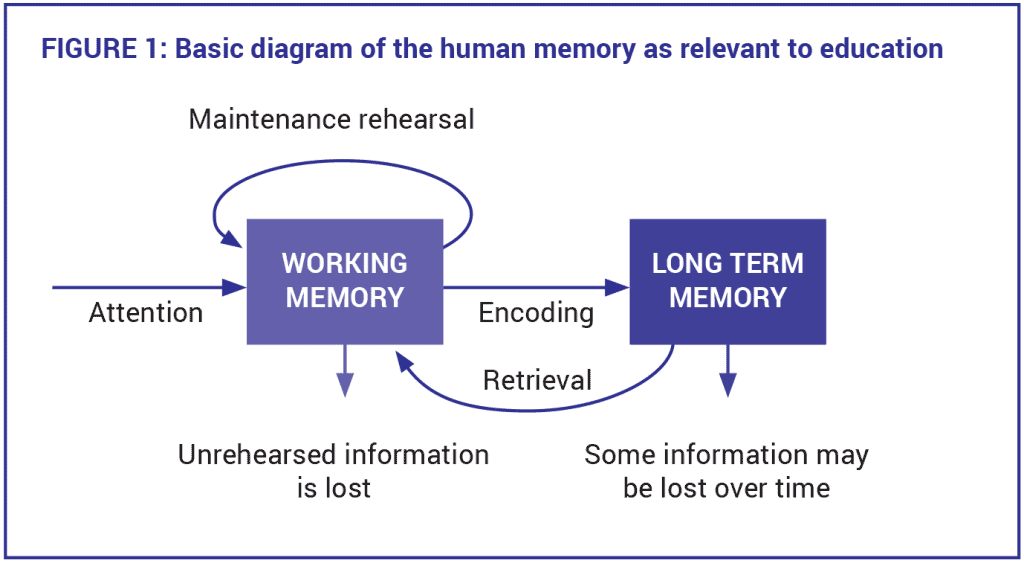
The general memory structure in Figure 1 shows that the memory system is not a unitary entity. In other words, it is not just one system but rather two memory components that do not function separately. These two components have links between them that represent separate processes.
Working memory is the conscious component of our memory where novel information is temporarily stored and actively manipulated for reasoning, learning and comprehension. For learning to occur, information must be processed in working memory for meaning before it is passed into long-term memory. Long-term memory is the unconscious component of our memory. If we have truly learnt something, it means we have stored it indefinitely in knowledge structures known as schemas in our long-term memory. Schemas are activated when learners deal with familiar information. When this trigger occurs, schemas are transferred from long-term memory to be consciously processed in working memory for a specific purpose. This happens automatically and easily because it is a biologically primary skill. A more knowledgeable learner in a domain can effortlessly transfer large amounts of organised schematic information from long-term memory to working memory to assist with carrying out complex problem-solving tasks because their schemas are more sophisticated in magnitude, complexity and refinement than those of a less knowledgeable learner.
Working memory has a limited capacity and can only remember roughly five to nine items or chunks of novel information at any one time[iv]. In addition, only two to four chunks of novel information can be simultaneously worked on or thought about in our working memory[v], which means that we can work on only a very limited number of items when a task requires working memory resources to process a new task. Furthermore, we can only hold this limited amount of information in working memory for about 20 seconds without needing to prompt our memory[vi]. The limitations of our working memory result in cognitive load whenever we are presented with new information.
Unlike working memory, long-term memory has no known limits. Furthermore, when familiar information is transferred from long-term memory back to working memory to be used for reasoning or problem solving, working memory has no limits on its capacity or duration. Working memory only has limits when dealing with novel information, not familiar information from long-term memory. Accordingly, when information is stored in long-term memory, the contents of our mind change – this is the process of learning.
Why is it so important for teachers to know about cognitive load theory?
Cognitive load theory is vital for teachers to know about and understand because it helps them reduce unnecessary cognitive load on students’ working memory in order to promote and optimise learning. A student’s competence in a specific domain is dependent on what is stored in their long-term memory. However, when a student does not have the prior knowledge to complete a task, and information about how to complete the task has not been provided, this creates the need for problem solving where novel information must be constructed. The newly generated information must be tested for its effectiveness, with ineffective information being removed and effective information kept, making the process of generating new information in working memory slow and difficult. This is not a very effective way of learning, but it is the only procedure available when solution paths such as information from teachers are unavailable.
This means that engaging in inquiry-based learning is usually an ineffective process for novice or less experienced learners because it imposes a considerable cognitive load on their working memory. Learners are forced to resort to weak, unguided methods such as problem solving, as in the example above where a novice algebra student attempts to solve 2x – 40 = 60 by randomly guessing the value of x. By contrast, when a less experienced learner in a specific domain studies the solution steps contained in a worked example prior to attempting a similar problem-solving task, this diminishes cognitive load and therefore efficiently assists the student to transfer knowledge of the method for solving the problem to long-term memory. A student who already holds domain-specific knowledge in long-term memory can use that knowledge to accurately categorise the problem and its solution. This is why problem solving (or inquiry-based learning) is better suited for more experienced learners, because they can perform the entire solution in a single mental step that imposes a minimal working memory load.
Cognitive overload occurs when the working memory resources needed to process a task are greater than available working memory resources. When working memory is overloaded, content is hard to understand, learning becomes slow or ineffective, and transferring knowledge into long-term memory becomes difficult. Students might experience cognitive overload when:
- they are exposed to complex learning material without being provided with sufficient guidance from teachers or educational materials (see the worked example effect below)
- they are required to split their attention among multiple sources of interrelated information (see the split-attention effect below)
- they are forced to process unnecessary information because it is integrated with essential information (see the redundancy effect below)
- the level of instructional guidance has not been adjusted to take into account their prior knowledge (see the expertise reversal effect below)
- they are exposed to a highly variable task, but they do not have a sufficient level of expertise to enable them to process the task (see the variability effectbelow)
What is the state of the evidence regarding cognitive load theory?
Over the last three decades, instructional techniques (known as cognitive load effects) have been developed within the framework of cognitive load theory to help people learn effectively. Each effect is based on multiple, replicated, randomised, controlled trials. Most of the early research on cognitive load effects was conducted in mathematics and science-based domains, although increasing amounts of research have been conducted more recently in non-scientific content domains such as music, literature, and foreign language acquisition. Consequently, cognitive load theory is well grounded in robust empirical evidence based on hundreds of randomised, controlled trials carried out by many researchers from around the world. This evidence suggests that cognitive load effects can be directly transferred to most learning environments. By taking a scientific approach to the way learning materials are designed, cognitive load theory and its associated effects help to alleviate cognitive overload and maximise learning.
Useful cognitive load effects to help you design and implement effective teaching strategies
As teachers, you can help overcome your students’ working memory limitations and foster effective learning by factoring in some of the following cognitive load effects.
The worked example effect
The worked example effect demonstrates that it is not effective to have novice learners (less experienced learners in a specific domain) attempt to solve problems without any instructional guidance. In the absence of substantial prior knowledge, novice learners will randomly generate their own solutions and test the effectiveness of them. This approach is likely to overload working memory capacity, cause a high cognitive load, and inhibit learning. Teachers can reduce unnecessary cognitive load and make learning more efficient by providing worked examples. Novice learners who are exposed to worked examples during the initial stages of cognitive skill acquisition learn more easily and more rapidly than they would when trying to solve the problem by randomly generating solutions: this is the worked example effect. It has been replicated on many occasions in technical domains such as mathematics, science, engineering, and computer programming, and to some extent in non-technical domains such as English literature, foreign language acquisition, athletics, music instruction, history, and social sciences.
Worked examples in technical domains essentially consist of a problem statement followed by a well-structured representation of solution steps that clearly specify how to solve a particular problem or perform a particular task. The most efficient way to present learning material for skill acquisition and application is to link the worked example to a similar target practice problem (known as a near transfer problem), rather than presenting an entire set of different worked examples followed by a set of varied practice problems. Alternating worked examples and problem solving enables the student to derive the full benefit of using appropriate prior information from the example to build rules for the similar problem to be solved. Solving a problem immediately after studying a similar worked example is also likely to generate more incentive for the student to study the original example.
Worked examples in non-technical domains are similar to the classical worked examples in technical domains. In the domain of English literature, for example, a worked example may consist of an essay question (which is analogous to the problem statement found in a mathematics problem) and a model answer to the essay question (analogous to the solution steps that specify how to solve a mathematics problem). The model essay can therefore be used as a general guide to help answer a similar type of essay question (analogous to studying a mathematics worked example and attempting to solve a near transfer problem).
The split-attention effect
Split attention occurs when multiple sources of information cannot be understood at the same time because the items of information are in a split-source format – in other words, disparate sources of information are not integrated to form one intelligible task. An example is shown in Figure 2 below, where a student is asked to solve an unknown angle in a geometric diagram and the explanatory written text is not placed next to the unknown angle nor is there an arrow pointing to the unknown angle. To make sense of the instructional material, the student will have to work out the relevant relationships by searching and matching between the written text and the corresponding parts of the diagram. This kind of cognitive activity will impose an unnecessary cognitive load because the written text must be mentally integrated with the diagram by reading it and then storing it in working memory temporarily before searching for the correct reference in the diagram. This unnecessary activity can overburden working memory and interfere with learning because of the intensive search-and-match process that is required for mental integration. In other words, the student’s working memory is fully occupied by integrating the visual and written information provided in the question and is unable to attend to solving the mathematical problem.
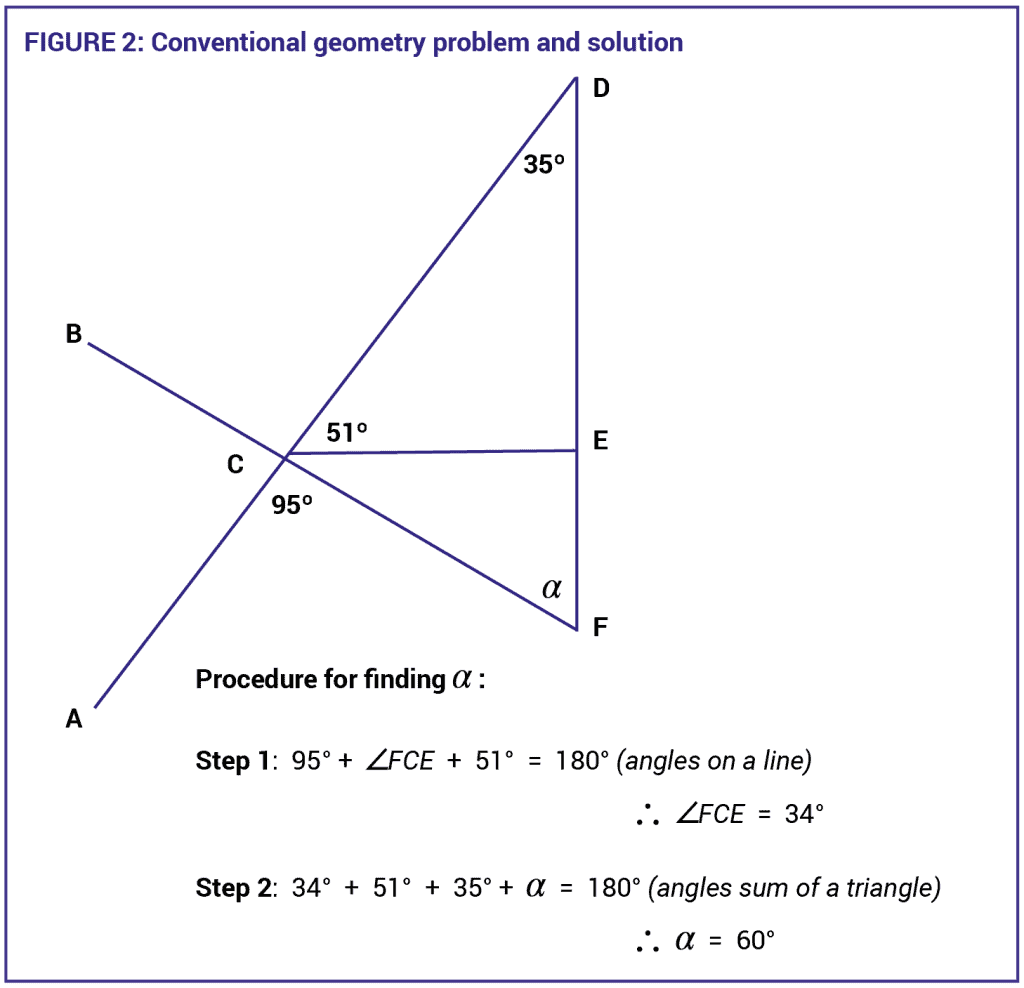
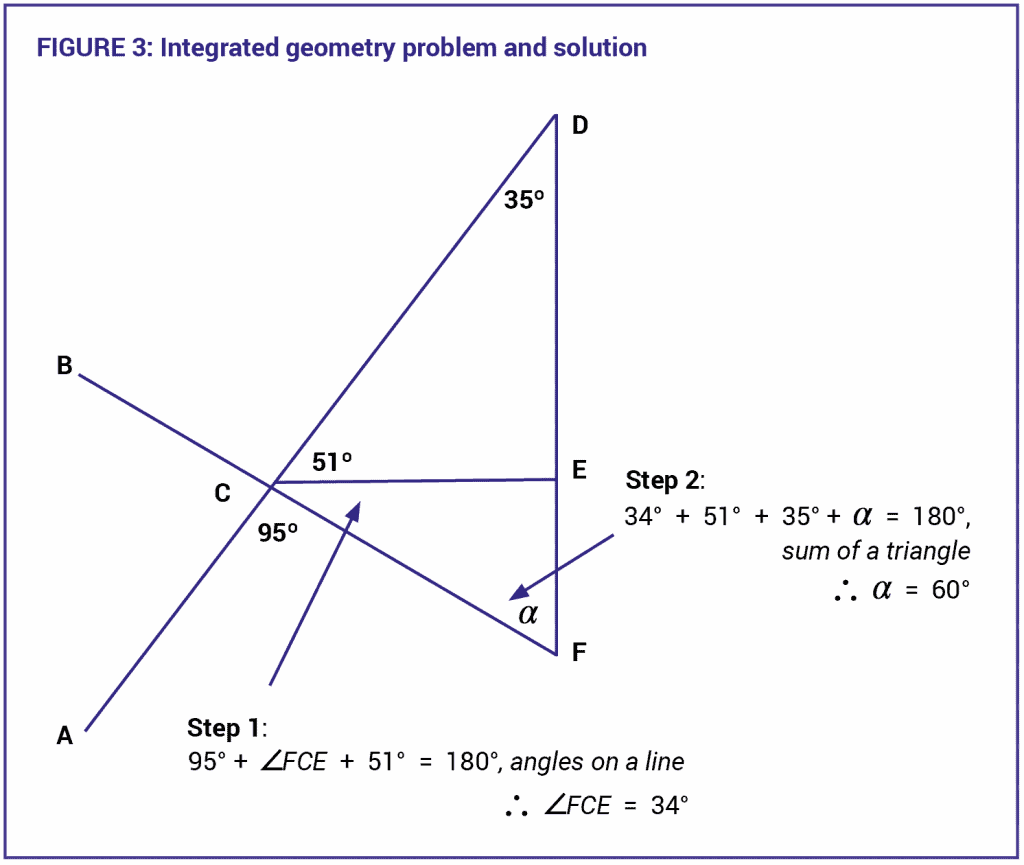
The heavy split-attention situation in Figure 2 can be reduced if the corresponding textual explanations are physically embedded into the components of the diagram as shown in Figure 3 below. When multiple representations of interdependent sources of information are integrated into a unified source of information, the student is not required to unnecessarily search for and match different sources of information to complete a task: this benefit is the split-attention effect. It applies not only to diagrams and texts but equally to any two interdependent sources of information such as text and tables, tables and diagrams, and so on.
The redundancy effect
When teachers provide additional information to students to help reduce their mental effort and alleviate unnecessary cognitive load, they may unwittingly include redundant information that has already been presented or is unnecessary for learning. The redundancy effectshows that providing students with redundant information can have a negative effect on learning because students are forced to process multiple lots of information together to make sense of it when they do not need to. Redundant information could include identical words in written and auditory form. For example, when a teacher reads out the exact words that appear on PowerPoint slides, this forces students to unnecessarily alternate between the written and spoken text, resulting in the text being read out of phase with the teacher’s speech. Removing some of the written text on PowerPoint slides and keeping the spoken text increases the likelihood of more information being absorbed.
Another case of redundancy occurs when teachers attempt to elaborate by providing additional information that is lengthy and unhelpful, such as integrating explanatory written text in a diagram when the diagram is intelligible on its own. Unlike the split-attention effect, where different sources of information that are unintelligible on their own should be integrated, teachers should avoid replicating necessary information into instructional materials. For example, any information that repeats what is being presented, such as simultaneous spoken and written text or written text that merely describes a diagram, should be eliminated. Similarly, any unnecessary information such as cartoons or music should be eliminated because, while this material may be interesting or engaging for students, it is unlikely to lead to learning and may in fact detract from the learning. Redundant information should be eliminated so that scarce working memory resources are not wasted on processing it.
The expertise reversal effect (prior knowledge effect)
There is a plethora of strong evidence to suggest that the effectiveness of many cognitive load effects depends on the level of learner expertise in a specific domain. For example, using worked examples is most effective for novice learners because they have not yet stored in their long-term memory the appropriate problem-solving knowledge structures relevant to the area being studied. However, worked examples lose their effectiveness when studied by more experienced learners in a domain, and may even hinder learning due to redundancy. The expertise-reversal effect shows that teaching strategies should be matched to an individual student’s level of expertise in order to promote knowledge acquisition – novice learners learn best from clear, explicit instructions (such as worked examples) and, as expertise increases, more experienced learners learn best from inquiry-based learning (such as unguided problem solving).
The variability effect
Studying multiple worked examples with the same solution structure can help students solve novel and difficult problems if they are able to draw an analogy between the examples. This is because learning can be enhanced if the tasks differ in their surface features (for example: 2y = 20; 2x = 20; 3x = 30; 4x = 40; 0.4x = 1) and not their structural features (for example: 2x = 20; 2x + 60 = 4x – 40; (2x)2 = 100.
When worked examples differ only in their surface features (in other words, they have a common solution structure), they enable students to recognise and reinforce the same solution steps.
Practising the same procedure with different variants of the task leads to the making of generalisations about the task. Generalising helps with the construction of (or the further development of previously constructed) schemas. These schemas enable learners to recognise the same task in future problems, despite any superficial elements that may vary the problem from those previously practised.
Consider a primary school mathematics problem: ‘Chloe has two marbles and Peter has three marbles. How many marbles do they have together?’ A low-variability problem would be: ‘Soula has two hats and Steve has three hats. How many hats do they have together?’ A high-variability problem would be: ‘A box has five small blue balls, four large green balls, six large red balls, and two small yellow balls. How many large balls are there altogether?’ In this example, the low-variability mathematical task varies only by way of the object (the marbles are replaced by hats), while the addition calculation of the numbers remains the same; and the high-variability mathematical task varies by way of the objects and the numbers. This enhances learning because students are able to create a generalised rule that can be transferred to a wider class of tasks that contain different surface features. Exposure to high-variability example-based instruction, compared to low-variability homogeneous examples, enables learners to engage in deeper processing which enhances the ability to transfer knowledge.
Research has confirmed that it is important to adapt instructional procedures to a student’s existing schematic knowledge base in their long-term memory (according to the expertise reversal effect discussed above). Accordingly, students should be initially presented with low-variability problems (to avoid cognitive overload), with variability increased as their levels of knowledge advance – in other words, more experienced learners should be presented with high-variability learning tasks[vii].
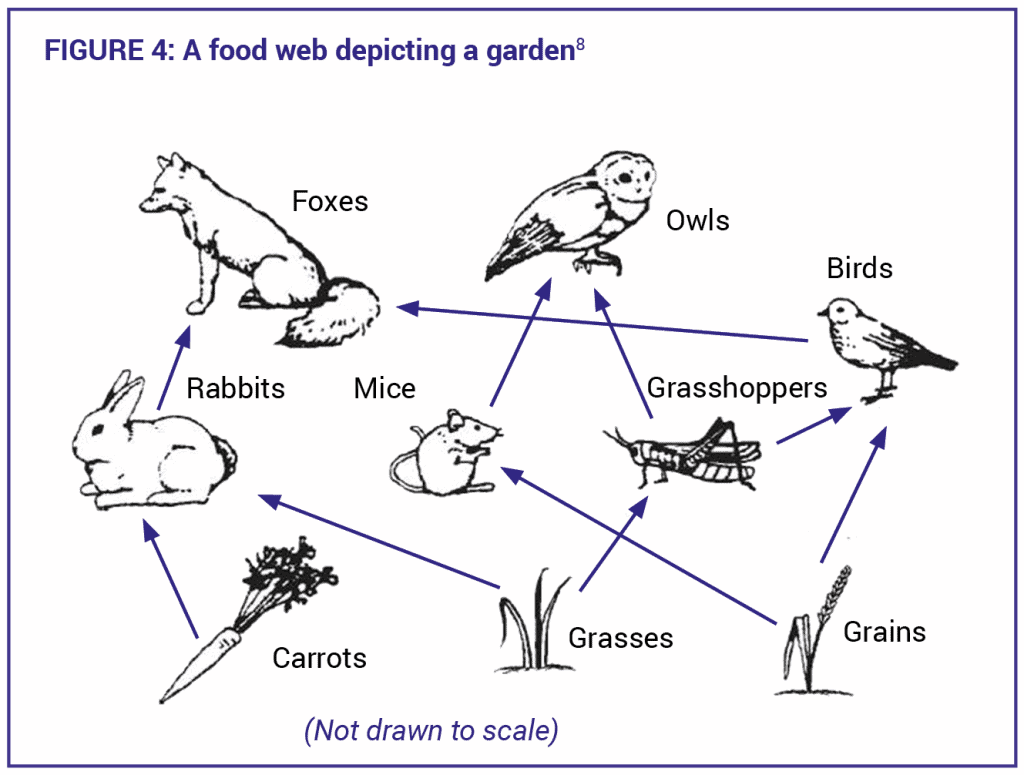
Consider a science lesson, where students are taught that energy in the form of food is transferred from one organism to another, and that scientists represent this transfer by using an arrow. Given that a fox is the predator and its prey is a rabbit, students could be given the example: carrots→rabbit→ fox. It is more effective to give a less experienced learner a low-variability problem such as: ‘Which animal is the predator and which is the prey in the food chain grains→mice→owl?’ On the other hand, a more experienced learner could be asked to study the diagram in Figure 4 and be given a high-variability problem such as: ‘Many food chains can be joined together to make a food web. Which animal is the prey AND the predator in this food web?’ The example provided for the low-variability problem allows the novice learner to learn which is the prey (rabbit) and which is the predator (fox). Once the novice learner can understand the food chain (which is just one single line), the teacher can move onto the food web diagram in Figure 4, which is much more challenging because of the many interconnected food chains that require the student to work out that the bird is a predator (grasses→grasshopper→bird) but is also the prey (grains→bird→fox).
References and further reading
Cowan, N. (2001). The magical number 4 in short-term memory: A reconsideration of mental storage capacity. Behavioural and Brain Sciences, 24(1), 87-114.
Garnett, S. (2020). Cognitive load theory: A handbook for teachers. Crown House Publishing.
Geary, D. C. (2008). An evolutionary informed science. Educational Psychologist, 43(4), 179-195.
Likourezos, V., Kalyuga, S., & Sweller, J. (2019). The variability effect: When instructional variability is advantageous. Educational Psychology Review, 31(2), 479-497.
Lovell, O. (2020). Sweller’s cognitive load theory in action. John Catt Educational.
Miller, G. A. (1956). The magical number seven, plus or minus two: Some limits on our capacity for processing information. The Psychological Review, 63, 81-97.
Peterson, L. R., & Peterson, M. J. (1959). Short-term retention of individual verbal items. Journal of Experimental Psychology, 58(3), 193-198.
Endnotes
[i] https://www.youtube.com/watch?v=gOLPfi9Ls-w&t=1s (Emeritus Professor John Sweller – UNSW, Sydney)
[ii] Geary, 2008.
[iii] Explicit instruction is the teaching of skills and concepts that uses direct, structured instruction which is designed and delivered to novices to help them develop specific knowledge about a topic.
[iv] Miller, 1956.
[v] Cowan, 2001.
[vi] Peterson & Peterson, 1959.
[vii] Likourezos, Kalyuga & Sweller, 2019.
[viii] Retrieved from https://desertoasisgarden.wordpress.com/2015/05/13/understanding-our-garden-better-with-a-food-web/#:~:text=A%20food%20web%20is%20a,5%20major%20levels%20of%20organisms.&text=Primary%20Consumers%3A%20Organisms%20that%20feed,autotrophs%2C%20also%20known%20as%20herbivores.
By Dr Vicki Likourezos

